This java applets let you understand the entire range of behavior of a single convex lens or image formed by two lens.

How to use it:

• You will see single convex lens and a block with four different at each corner.
• You will also find images for those corner.
• It is like viewing the image of a 3 dimensional object.
• The image is distorted and its length is reduced more than its height.
• The magnification transverse to the axis is greater than the longitudinal magnification along the axial direction.
• Click within the area of the block will show light path for different points.
• The location for the object p and object q are shown near the top, the focus length are labeled at the bottom.
• You can click within the small circle at the focus point and drag the mouse to change the focus point.
• Click at the top left corner of the block and drag the mouse to move it.
• Click the bottom right corner of the block and drag it to change its size.
• The mouse position is displayed as ( x, y ) value.
• Click the right mouse button to have another lens, Click it again to remove it.
• x2 is the location of the mouse tip relative to d is the distance between two lens.
• You will find image formed by two lens.
• Click within lens area and drag the mouse to move the lens. Click the circle between lens to change the focus length.
• You can simulate image formed by lens combination experiments with this java applets. All the related parameters are shown, record it and perform a virtual experiment.

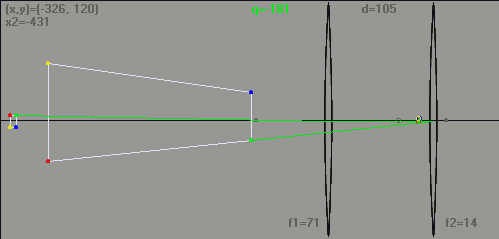
Emulate refracting telescope: Enlarge the image of a distant object. The object is at a finite far distance from the device, so that the intermediate image is located beyond the image focus of the objective. The inverted intermediate image served as the object for the eyepiece,which function as a magnifier. Magnifying power = f1 / f2

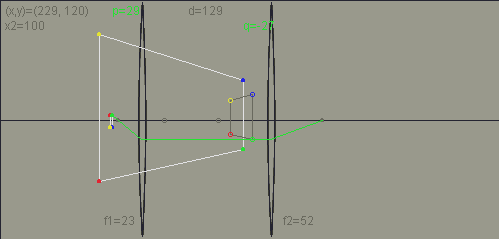
Emulate compound microscope: The lens system closest to the object is the objective. It forms a real, inverted, magnified image of the object that is then viewed by the eyepiece. The latter is essentially a magnifying glass that looks at and enlarge the image created by the objective. The total angular magnification od the system    = d * 25.4(cm)/ (f1 *f2)

---

Your suggestions are highly appreciated!  E-mail: Click hwang@phy03.phy.ntnu.edu.tw
Author: Fu-Kwun Hwang Dept. of Physics  National Taiwan Normal University
Last modification time:  
Back to Optical